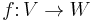Mazur–Ulam theorem

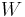In mathematics, the Mazur–Ulam theorem states that if $V$ and $W$ are normed spaces over R and the mapping

$f\colon V\to W$

is a surjective isometry, then $f$ is affine.

References

Richard J. Fleming; James E. Jamison (2003). Isometries on Banach Spaces: Function Spaces. CRC Press. p. 6. ISBN 1584880406.
Stanisław Mazur; Stanislaw Ulam (1932). "Sur les transformationes isométriques d’espaces vectoriels normés". C. R. Acad. Sci. Paris 194: 946–948.

External links

A proof (PDF)

‹The stub template below has been proposed for renaming to . See stub types for deletion to help reach a consensus on what to do.
Feel free to edit the template, but the template must not be blanked, and this notice must not be removed, until the discussion is closed. For more information, read the guide to deletion.›